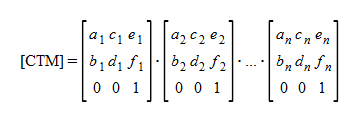
Non Scaling Objects / constrained transforms

This proposal was built for the follow ups of a series of discussion (listed below) about Non Scaling functions.

Using this proposal, it is discussed at seattle F2F.

Vecotr Effect Ext. Proposal latest

Issues

I (stakagi) am looking at two issues toward the ref(svg*) specification of SVGT1.2.

Somewhat difficult and special description
Lack of the consideration to nested documents

Basic Transformations Formula

This is definition for CTM from 7.5.

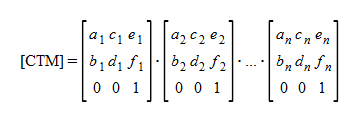
Transformation formula to viewport Coordinate System is also defined.

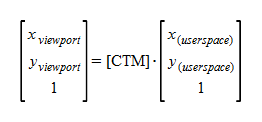
On the other hand, a formula for the coordinate system of the device may be as follows.
# x(userspace), y(userspace) is abbreviated as x, y.

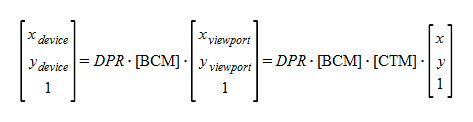
Here, DPR is Device Pixel Ratio (scalar). And [BCM] presupposes that it is a matrix synthesizing the coordinate transformation by Browser Chrome's built-in zooming panning functions. [References:1]

SVGT1.2: ref(svg,x,y) and ref(svg)

Based on these formulas, transform="ref(svg, x, y)" which SVGT1.2 says may be following. (if I don't misunderstand...)

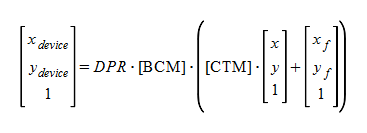
<circle transform="ref(svg,x,y)" cx="xf" cy="yf" r="rf"/>

x and y are the corresponding values in ref(svg, x, y), and xf and yf are the coordinate valuess as the graphics element in which ref(svg was declared, including its descendant.
xf and yf are not influenced even if CTM changes for zooming or panning. This offers an effect like the icon on a map, for example. It is an object from which size does not change, although a place changes according to zooming and pannning.

And transform="ref(svg)" which SVGT1.2 says may be following.

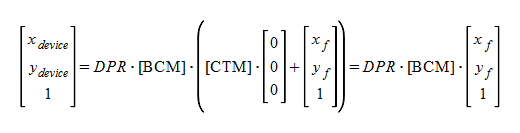
<circle transform="ref(svg)" cx="xf" cy="yf" r="rf"/>

This provides an effect like the introductory notes in graph, for example. As for it, neither a place nor size changes.

Proposal of change of the description

How about extending to vector-effect for a similar function in which the implementation to browsers has already advanced?

for ref(svg,x,y)

change from

<circle transform="ref(svg,100,100)" cx="10" cy="5" r="30"/>

<g transform="translate(100,100)">
  <circle vector-effect="additional-fixed-coordinates" cx="10" cy="5" r="30"/>
</g>

Here, the coordinates of the target graphics primitive are assumed to have been consumed as xf and yf (5 and 30 in this example), and it is also assumed that x and y values of that graphic are always 0. On the other hand, with this sample, e and f of CTM is set to 100,100 by transform of the 'g' element which is parents. Therefore, the same behavior as the example using ref(svg, 100, 100) is shown.

for ref(svg)

change from

<circle transform="ref(svg)" cx="100" cy="100" r="30"/>

<circle vector-effect="fixed-coordinates" cx="100" cy="100" r="30"/>

Fixed object for nested documents

However, the non-scaline characteristic will be transmuted when nested document embedding is performed.

This is formula for nested documents. CTMroot is CTM of a root document and CTMdecendant* are CTMs of the descendants.

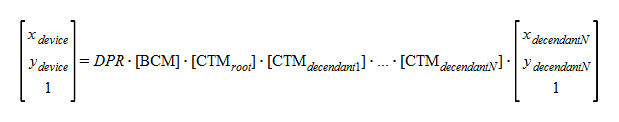
The following formulas will be made by applying ref(svg, x, y) to the last descendant.

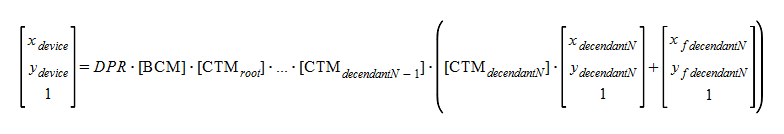
If we change CTMroot for zooming and pannning, the fixed characteristic will be lost since xf,yf are still influenced by CTMroot, CTMdecendant1...CTMdecendantN-1s. So fixed characteristics are secured only if you change this document's CTM. For example, in the maps piled up by nested documents (layered maps), this may become a issue.

Therefore, fixed functionality applied toward a root document is also required. The formula may become following.

Here, xg and yg are the additional coordinate values which are fixed toward a root document.

The same subject can be said also toward ref (svg). Namely, non-scaling only for this document;

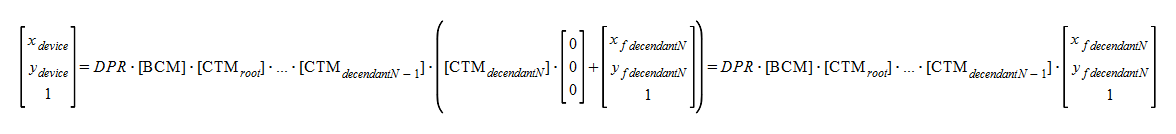
And non-scaling entire nested documents;

As a result, the value of non-scaling may be extended such as follows.

vector-effect="additional-fixed-coordinates-root"
vector-effect="fixed-coordinates-root"

Moreover, fixed features which cancels even transformation by Browser Chrome [BCM] is investigated further.

Syntax

According to css3 'box-shadow' property and css3 'text-shadow' peoperty, grammar for multiple values which has multiple parameters are well known as css property value. Therefore, it will be relevant for the future method of extending for giving various functions to the 'vector-effect' property to follow them.

vector-effect='val1_param1 val1_param2 , val2_param1 val2_param2 val2_param3 , val3_param1 val3_param2'

Polyfills

Almost complete polyfill without screen CTM option : On occasions when an element with a vector-effect property also has a transform property, spec says that only when there is a fixed-position value, it seems to use only e and f values of that transform property and other cases throws. The spec should show this point more clearly.
Screen attribute was implemented for trial

CSS3 scaleX,scaleY application instead of coordinatwe system's scale:sqrt(abs(det))

ISSUE: If skew is applied, non-scaling functionality is not performed. See Polyfill